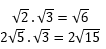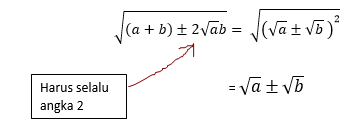Cara Menyederhanakan Bentuk Akar

Sebelum belajar menyederhanakan bentuuk akar, pertama-tama kita harus faham apa itu akar, dan bagaimana operasinya. Tapi, kali ini saya tidak akan menjelaskan apa itu akar, karena harusnya ade’-ade’ sudah mengerti ( kalo ngg’ ngerti tanya ama yang ngerti ʅ ( ¯ 3 ¯ ) ʃ ). Saya hanya akan membahas operasi-operasi pada bentuk akar karena ini merupakan dasar dari penyederhanaan bentuk akar.

1.        Operasi penjumlahan dan pengurangan

Dalam bentuk akar, kita hanya boleh menjumlahkan atau mengurangkan akar-akar yang bilangannya sama dan kebanyakan siswa salah dalam hal ini. Bilangan akar, bisa diibaratkan sebagai sebuah variabel. Misalnya variabel x atau y. Nah, ketika kita menjumlahkan x dengan x, maka kita bisa menuliskannya menjadi 2x tapi, ketika kita menjumlahkan x dengan y, kita tidak boleh kan menuliskannya dengan xy atau 2 xy tapi kita tetap menuliskannya dengan x + y. Bilangan akar juga memiliki aturan yang sama. agar ade’- ade’ tidak bingung, langsung saja kita lihat contohnya :

 

1.    Operasi perkalian dan pembagian

Kalau untuk operasi yang satu ini kita boleh mengalikannya langsung di dalam akar. Lebih mudah kalau langsung ke contoh :

Kalau udah faham sama yang di atas, kita tinggal belajar menyederhanakan suatu bentuk akar.

Untuk menyederhanakan suatu bentuk akar, biasanya menggunakan 3 jenis penyelesaian yaitu :

Agar ade’-ade’ tidak bingung, kita akan bahas satu per satu ( ʼ ᴗ ʽ )

 

Biasanya untuk menyederhanakan suatu bentuk akar, kita harus merasionalkan bentuk akar tersebut terlebih dahulu. tapi, apa itu bilangan rasional ? sederhananya, bilangan rasional itu adalah bilangan yang yang penyebutnya adalah bilangan bulat. Contohnya : 

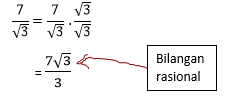
Nah, untuk menyederhanakan soal yang seperti ini, kita cukup mengalikan pembilang  dan penyebutnya dengan penyebut dari bilangan tersebut. Hmm..lagi-lagi teorinya membingungkan ya? ( X _ X ).yah, kira-kira begini simulasinya :

Misalnya ada soal penyederhanaan seperti ini :

 

Soal di atas bisa kita tulis seperti ini :

Karena angka 1 bisa didapat dari pembagian antara 2 angka yang sama misalnya 2 dibagi 2 atau 6 dibagi 6 asalkan angkanya sama, maka hasilnya akan sama dengan 1. Jadi :

 

Sekarang bagaimana jika soalnya seperti ini : 

Jika soalnya seperti itu, kita cukup mengalikannya dengan bentuk akarnya saja

Untuk yang satu ini hampir sama dengan yang tadi, bedanya untuk bentuk yang satu ini penyebutnya memiliki operasi penjumlahan/pengurangan. Nah, dalam operasi penjumlahan/pengurangannya tidak harus keduanya memiliki bentuk akar, bisa saja salah satunya adalah bilangan bulat contohnya :

  

Jadi, apakah cara penyederhanaanya sama dengan bentuk yang pertama ?. yah, kurang lebih hampir sama hanya saja operasi yang ada pada penyebutnya berubah menjadi kebalikannya. Contohnya :

Sebenarnya ada cara singkat ketika mengalikan penyebut tadi :

  

Tapi ingat, trik ini hanya berlaku untuk perkalian antara operasi yang berbeda yang berbeda ( ʽ Δ ʼ ). klo untuk perkalian dengan operasi yang sma trik nya beda lagi contoh nya :

 

bentuk yang satu ini digunakan jika soalnya meiliki operasi penjumlahan/pengurangan bentuk akar di dalam akar, jadi seperti kotak di dalam kotak atau mungkin lebih cocok monster di dalam monster( X _ X ).  Contoh soal :

  

Untuk menyelesaikan soal seperti itu, kita harus jeli melihat soal, bagaimana caranya  agar soal dapat kita ubah menjadi bentuk

Jika bentuk soalnya sudah seperti di atas, maka soal sudah pasti dapat terselesaikan. Nah, jadi kenapa bentuk soalnya harus seperti itu ? coba lihat simulasinya :

Nah, berdasarkan simulasi di atas, berarti :

Jadi, kita harus bisa mengubah bentuk soalnya. Contoh :

nah, jadi sekian dulu materi tentang bentuk akar, kalau ada yang kurang jelas silahkan tinggalkan komentar.